Forschung

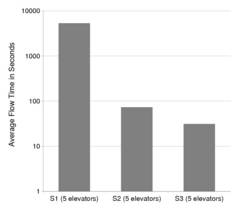
Mit heuristischer (S2), aber vor allem mit mathematischer Optimierung (S3) können gegenüber üblichen Methoden (S1) bei Spitzenbelastung die Beförderungszeiten eines Lastenaufzugs reduziert werden.

Forschungsschwerpunkt des Lehrstuhls für Wirtschaftsmathematik ist die Diskrete Optimierung sowie die zugehörige Grundlagenforschung in der Analyse von Algorithmen und diskreter Mathematik. Eingesetzt werden die Verfahren der diskreten Optimierung insbesondere in den Bereichen der Telekommunikation, Logistik und Verkehr.

Jörg Rambau ist momentan Direktor des Forschungszentrums „Modellierung und Simulation (MODUS)“ der Universität Bayreuth, in dem einige Projekte des Lehrstuhls eingebettet sind.

Die meisten Optimierungsprobleme in der Praxis sind dynamisch. Es reicht nicht aus, einen Ablaufplan einmalig zu optimieren und dann fortwährend zu verwenden. Stattdessen muss während des Ablaufs eines Prozesses laufend ereignisbasiert optimiert werden. Man spricht hier von Online-Optimierung. Da eine solche Optimierung in der Regel berechnet werden muss, während das System läuft, muss ein Optimierungsverfahren stets ausreichend schnell eine Antwort liefern, damit das System nicht durch Warten zu stark verzögert wird. Dies bezeichnet man als Echtzeit-Anforderung.

Wir verwenden zur Modellierung in der Hauptsache Stochastische Ganzzahlige Lineare Optimierung und Markovsche Entscheidungsprobleme sowie die Theorie der Online-Algorithmen im engeren Sinne.

Zu jedem Zeitpunkt muss ein optimaler Einsatzplan für ADAC-Fahrzeuge vorliegen, der alle Aufträge abdeckt.

Beispiele für Online-Optimierungsaufgaben mit Echtzeitanforderungen, mit denen wir uns beschäftigt haben, sind die Einsatzplanung von Hilfefahrzeugen für den ADAC, die Steuerung von Lastenaufzugsystem oder die Außendienstplanung für Service-Techniker. 

Seit einiger Zeit interessieren wir uns auch für Planungsaufgaben, bei denen Schwierigkeiten wegen unvollständiger Information über die Zukunft auftreten: Für den großen Textildiscounter NKD erforschten wir, wie die Waren in Anbetracht einer schwer schätzbaren Nachfrage am besten auf Konfektionsgrößen und (über eintausend) Filialen verteilt werden sollten, damit der erwartete Ertrag maximiert wird.

Seit einigen Jahren beschäftigen wir uns auch mit Sportspiel-Strategie-Optimierung. Wann z. B. sollte man beim Beachvolleyball riskant und wann weniger riskant spielen in Anbetracht der Fähigkeiten der beteiligten Teams?

Im Gebiet zugrundeliegender mathematischer Strukturen arbeiten wir an Enumerationsverfahren für geometrische Objekte. Das Programmpaket TOPCOM ist seit mehr als 20 Jahren der Standard zur Enumeration von Triangulierungen von Punktkonfigurationen.